Площадь треугольника

Существует несколько формул для вычисления площади треугольника. Рассмотрим те, что изучаются в школе.

Первая формула вытекает из формулы площади параллелограмма и предлагается учащимся в виде теоремы: площадь треугольника равна половине произведения его основания на высоту.

Доказательство: пусть S – площадь треугольника АВС (см. рис. 5). Примем сторону АВ за основание треугольника и проведем высоту СН. Докажем, что .

Достроим треугольник АВС до параллелограмма АВDС так, как показано на рисунке 5:

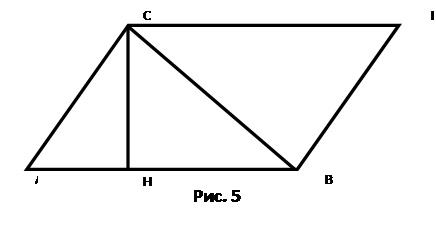
Треугольники АВС и DСВ равны по трем сторонам (ВС – их общая сторона, АВ=СD и АС=ВD как противоположные стороны АВСD), поэтому их площади равны. Следовательно, площадь S треугольника АВС равна половине площади параллелограмма АВСD, то есть . Теорема доказана.

Важно обратить внимание учащихся на два следствия, вытекающих из данной теоремы. А именно:

1) площадь прямоугольного треугольника равна половине произведения его катетов.

2) если высоты двух треугольников равны, то их площади относятся как основания.

Эти два следствия играют важную роль в решении разного рода задач. С опорой на данную доказывается еще одна теорема, имеющая широкое применение при решении задач: если угол одного треугольника равен углу другого треугольника, то их площади относятся как произведения сторон, заключающих равные углы.

Доказательство: пусть S и S1 – площади треугольников АВС и А1В1С1, у которых углы А и А1 равны (см. рис. 6).

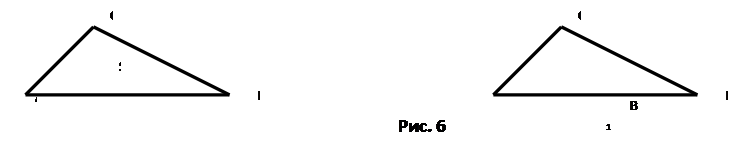
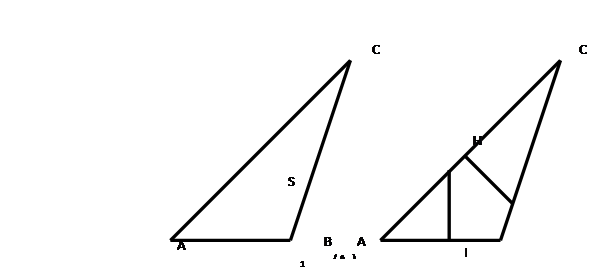
Докажем, что

Наложим треугольник А1В1С1 на треугольник АВС так, чтобы вершина А1 совместилась с вершиной А, а стороны А1В1 и А1С1 наложились соответственно на лучи АВ и АС. Треугольники АВС и АВ1С имеют общую высоту СН, поэтому Треугольники АВ1С и АВ1С1 также имеют общую высоту - В1Н1, поэтому 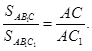Перемножая полученные равенства, находим: или . Теорема доказана.

Вторая формула тоже связана с параллелограммом: Площадь треугольника равна половине произведения двух его сторон на синус угла между ними. Существует несколько способов доказательства этой формулы и один из них – достраивание треугольника до параллелограмма.

Докажем, что . Достроим треугольник АВС до параллелограмма АВDС (см, рис. 7)

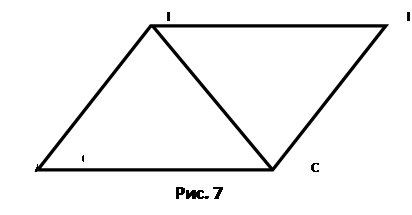
Треугольники АВС и DСВ равны по трем сторонам (ВС – общая сторона, АВ=DС, АС=DВ как противолежащие стороны параллелограмма). Площадь параллелограмма можно найти по формуле . Тогда по основным свойствам площади площадь треугольника АВС равна . Что и требовалось доказать.

Третья формула для площади треугольника – формула Герона названа так в честь древнегреческого ученого Герона Александрийского, жившего в первом веке нашей эры. Эта формула позволяет находить площадь треугольника, зная его стороны. Эта формула удобна тем, что позволяет не делать никаких дополнительных построений и не измерять углов. Ее вывод основывается на второй из рассмотренных нами формул площади треугольника и теореме косинусов:

Информация по педагогике:

Методика разработки и структура образовательных проектов в физическом воспитании школьников
В настоящее время проектирование является актуально значимым понятием в педагогике и образовательной практике. Его появление и успешная экспансия в образовательном пространстве связаны с именами таких ученых и методологов, как Н.Г. Алексеев, О.С. Анисимов, Ю.В. Громыко, В.П. Беспалько, В.В. Давыдов ...

Особенности психического развития детей раннего и дошкольного возраста с нарушениями слуха
Нарушения слуха в раннем и дошкольном возрасте оказывают особенно сильное влияние на последующее развитие ребенка. В сложной структуре развития ребенка со сниженным слухом наряду с первичным недостатком слухового анализатора отмечается своеобразие в формировании его речи и других психических процес ...

Структура игры
Из предыдущего параграфа стало ясно, что понятие «игровые педагогические технологии» включает достаточно обширную группу методов и приемов организации педагогического процесса в форме различных педагогических игр. Давайте выясним, как определяют игру известные педагоги, психологи, писатели различны ...