Площадь криволинейной трапеции

Криволинейной называется трапеция, одна из боковых сторон которой – отрезок кривой.

Нахождение площади криволинейной трапеции рассматривается в школе как одно из применений интеграла. При рассмотрении геометрического смысла интеграла [4] в 11 классе в учебнике так и говорится: «Коротко об интеграле можно сказать так: Интеграл – это площадь». Далее следует определение интеграла:

«Пусть дана положительная функция f

определенная на конечном отрезке [a,b]. Интегралом от функции f

на отрезке [a,b] называется площадь ее подграфика». «Подграфиком» здесь называется фигура, ограниченная графиком функции f

,

прямыми x=a и x=b и осью абсцисс, то есть криволинейная трапеция.

Идея нахождения площади криволинейной трапеции заключается в разбиении ее на множество прямоугольников. По свойству аддитивности площади, площадь криволинейной трапеции приближенно равна сумме площадей прямоугольников. Точное же значение площади криволинейной трапеции находят, переходя от суммирования к интегрированию.

Задача: Найти площадь фигуры, заключенной между дугами парабол и .

Решение: Данная фигура ограничена графиками двух функций и , которые пересекаются в точке (1,1). Искомая площадь есть разность площадей криволинейных трапеций и .

Аналитически это можно записать как разность двух интегралов:.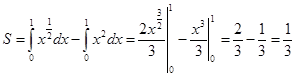

Теперь попытаемся подытожить и обобщить все вышесказанное. Среди различных систем величин, изучаемых в школе на различных этапах обучения, учащиеся уже в начальной школе знакомятся с понятием площади плоской фигуры. На первых этапах обучения речь идет об интуитивном представлении о площади, а не о строгом математическом обосновании этого понятия.

Первоначально у учащихся представление о площади плоской фигуры связывается с подсчетом числа единичных квадратов. Изучение площади в школе начинается с рассмотрения площади прямоугольника (стороны которого соизмеримы с линейной единицей измерения). Программа курса геометрии предусматривает знакомство учащихся с вычислением площади с помощью палетки. Использование ее позволяет сделать не только доступным для учащихся изучение вопроса об измерении площади любой плоской фигуры, но и помогает им правильно понять идею измерения площади (подсчет числа единичных квадратов, помещающихся в данной фигуре). Переходя от непосредственного измерения площади путем сравнения ее с единицей измерения к способам косвенного измерения площадей, учителю необходимо обратить внимание учащихся на то, что для измерения площадей нет столь удобных приборов, какие были для измерения длин отрезков и величин углов. Поэтому стоит более внимательно разобраться с величиной – площадью и выявить способы ее нахождения

.

Сравнивая свойства площади со свойствами таких величин, как расстояние, угол, мы убеждаемся в том, что:

а) площади можно складывать между собой и умножать на положительные числа;

б) за единицу измерения площади можно выбрать некоторую площадь S, где S=ku, где k – некоторое число, u – единица площади.

С понятием «Площади фигур» впервые учащиеся знакомятся в курсе геометрии V класса. Понятие площади фигуры вводится аксиоматически, но делается это неявно, с опорой на жизненный опыт учащихся. Сначала вводится формула площади прямоугольника (с целыми длинами сторон; длины сторон – конечные десятичные дроби; длины сторон – бесконечные десятичные дроби). На ее основе выводится формула площади параллелограмма; последняя выводится при выводе формул площади треугольника: ; (вводится немного позднее); , трапеции, выпуклого многоугольника, описанного около круга; должное внимание уделяется формуле площади круга; формула выводится неявно на уровне наглядных представлений; VII – IX классы – основа – предельный переход от площади правильных вписанных и описанных n-угольников к площади круга. Рассматриваются такие площади подобных фигур: зависимость площади подобных фигур от отношения их линейных размеров; соответствующее соотношение выводится и для простых фигур с помощью разбиения их на конечное число треугольников.

Информация по педагогике:

Структура математической игры
Математическая игра имеет устойчивую структуру, которая отличает ее от всякой другой деятельности. Основными структурными компонентами математической игры являются: игровой замысел, правила, игровые действия, содержание, оборудование, результат игры. Остановимся более подробно на отдельных структур ...

Использование экологических интернет-ресурсов в образовательном процессе
В последние годы в связи с развитием и широким внедрением в образовательную практику новых информационных технологий, мультимедийных средств и интернет-технологий значительно расширились рамки и возможности педагогических методик, применяемых в экологическом образовании. В связи с этим представляет ...

Сущность понятия «монологическая речь» и ее психологические особенности
Отношение к самому существованию и соответственно определению монологической речи у психологов и лингвистов далеко неоднозначно. Академик Л. В. Щерба условно считал монолог в значительной степени «искусственной формой», полагая, что «подлинное свое бытие язык обнаруживает лишь в диалоге». В то же в ...