Теоретические основы обучения математике в развивающей программе «Школа 2000…»

Понятие множества является одним из основных понятий математики и поэтому не определяется через другие. Его поясняют на примерах. Так, можно говорить о множестве букв в некотором слове, о множестве однозначных чисел.

Объекты, из которых образуется множество, называют его элементами.

В математике изучают не только те или иные множества, но и связи, отношения между ними.

Если множества А и В имеют общие элементы, т.е. элементы принадлежащие одновременно А и В, то говорят, что эти множества пересекаются. Если множества не имеют общих элементов, то говорят, что они не пересекаются.

Если каждый элемент множества В является элементом множества А, то говорят, что В – подмножество А, и пишется ВÌ А.

Множество В называется подмножеством множества А, если каждый элемент множества В является также элементом множества А. пустое множество является подмножеством любого множества (Æ Ì А). любое множество является подмножеством самого себя (А Ì А).

Продолжим рассмотрение отношений между множествами. Если каждый элемент множества В является элементом множества А и, наоборот, каждый элемент множества А является элементом множества В, то говорят, что множества А и В равны, и пишут: А=В.

Множества А и В называются равными, если А Ì В и В Ì А.

Из определения равных множеств вытекает, что равные множества состоят из одних и тех же элементов и порядок записи элементов множества не существен.

Все пустые множества равны.

Отношения между множествами наглядно можно представить с помощью кругов Эйлера. В том случае, если множества А и В имеют общие элементы, но не одно из них не является подмножеством другого, их изображают так, как это показано на рисунке 1.

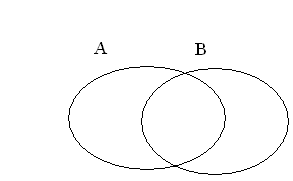
рисунок 1.

Непересекающиеся множества А и В представляют при помощи двух кругов, не имеющих общих точек (рис.2).

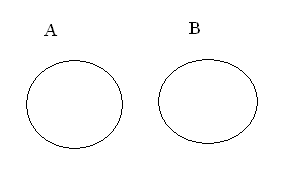рисунок 2.

Если множество В является подмножеством А, то круг, изображающий множество В, целиком помещается в круг, изображающий множество А (рис.3).

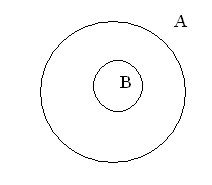
рисунок 3.

Равные множества представляют в виде одного круга (рис.4).

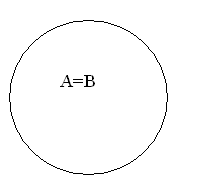
рисунок 4.

В математике часто приходится решать задачи, которые связаны с нахождением общих элементов двух или более совокупностей или с объединением нескольких совокупностей в одну. Обобщением таких ситуаций являются операции пересечения и объединения множеств.

Пересечением множеств А и В называется множество, состоящее из тех или только этих элементов, которые принадлежат как множеству А, так и множеству В.

Пересечение любых множеств А и В всегда существует и оно единственно.

Если представить множества А и В при помощи кругов Эйлера, то пересечение данных множеств изобразится закрашенной областью (рис.5).

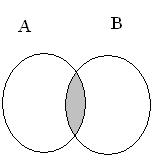
рисунок 5.

В том случае, когда множества А и В не имеют общих элементов, то говорят, что их пересечение пусто и пишут: А Ç В = Æ.

Операция, при помощи которой находят пересечение множеств, называется так же пересечением.

Объединением множеств А и В называется множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств Аи В.

Объединение любых множеств А и В всегда существует, и оно единственно.

Объединение множеств А и В обозначают: А È В.

Если представить множества А и В при помощи кругов Эйлера, то объединение данных множеств изобразится закрашенной областью (рис.6).

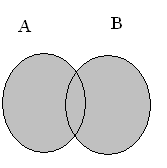
рисунок 6.

Операция, при помощи которой находят объединение множеств, называется также объединением.

Информация по педагогике:

Эстетический потенциал математики как науки
Эстетический потенциал математики в практике обучения часто недооценивают. Однако на протяжении веков пути математики и различных видов искусства переплетались. Поэтому исторические сведения предоставляют благодатный материал для развития эстетического вкуса школьников. Зачастую в кругу цифр и мате ...

Географическое состояние подготовки к ЕНТ
С 2006 г. при определении содержания экзаменационной работы учитываются не только обязательные минимумы содержа­ния основного общего и среднего (пол­ного) общего образования по географии, но и тре­бования к подготовке выпускников, за­фиксированные в Федеральном компо­ненте государственных стандарто ...

Особенности и этапы формирования восприятия картин пейзажной живописи у детей старшего дошкольного возраста
Восприятие представляет собой процесс непосредственного контакта с окружающей средой, процесс переживания впечатлений о предметах в рамках социоэмоционального развития наблюдателя. Это сложный психологический процесс. Он состоит из основных этапов: Афферентный синтез (анализ свойств объекта и предм ...