Роль и место понятия «площадь в школьном» курсе математики

Для корректного определения площади многоугольников — функции S(F) — требуется доказать, что такая функция существует и единственна.

Многим сам вопрос (об определении площади) покажется искусственным: они скажут, что площадь — первичное понятие, не подлежащее определению.

Взгляд на площадь как на первичное понятие сложился еще в древности. До недавнего времени этого взгляда придерживались и математики. На протяжении многих столетий они видели задачу в вычислении площадей; им не приходило в голову, что «площадь» нуждается в специальном определении.

Между тем их вычисления должны были на чем-то основываться — если не на прямом определении, то на чем-то, его заменяющем, на каких-то принципах, которые позволяли им всякий раз получать в качестве площади определенное число. И такие принципы, конечно, существовали, хотя обычно не формулировались. Это — основные свойства площади. Так, в школьных учебниках площадь многоугольников вообще не определяется, но указываются ее свойства, соответствующие аксиомам площади, или определения носят формально дескриптивный характер, но свойства, определяющие площадь, используются не для построения общей функции S(F) (об этом речи нет), а для вычисления площади основных плоских фигур: прямоугольника, параллелограмма, треугольника, трапеции и плоских фигур, составленных из этих основных.

Познакомившись с понятием «площадь» в пятом классе и научившись измерять площадь плоских фигур непосредственно (путем подсчета единичных квадратов, умещающихся в данной фигуре), учащиеся сталкиваются с проблемой неточности при таком способе измерения. Здесь вводится так называемый косвенный метод измерения площади. То есть площадь не измеряется, а вычисляется по какой-то формуле. И поэтому на протяжении всего курса математики школьники учатся не измерять, а вычислять площади плоских геометрических фигур с помощью формул.

На протяжении всего курса математики школьники учатся измерять площади плоских геометрических фигур. И чем больше различных геометрических фигур знают учащиеся, тем больше различных формул и способов вычисления площади им необходимо и тем больший математический «арсенал» для этого нужно задействовать. Возьмем, к примеру, прямоугольник. Для вычисления его площади необходимо всего лишь уметь умножать: . То же самое и в случае параллелограмма: . Далее: треугольник: – уже немного сложнее. При вычислении площади круга учащимся нужно уметь находить квадрат числа и знать отношение длины окружности к ее диаметру: . Площадь параллелограмма и треугольника можно вычислить и другим способом, но для этого нужно знать тригонометрию: , . Еще одним простым алгоритмом нахождения площади треугольника является формула Герона: . Для ее реализации учащиеся должны уметь извлекать квадратный корень из числа. Наиболее универсальной из всех школьных формул для вычисления площади является интегральная формула площади криволинейной трапеции: 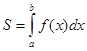. Но она и наиболее сложна – интегрирование часто вызывает у учащихся некоторые затруднения.

Информация по педагогике:

Педставления умственно отсталого ребенка о природе
Ориентация дошкольного учреждения на общечеловече­ские ценности значительно меняет при­оритеты в воспитании, направляя основ­ное внимание на комплексное развитие личности ребенка. Одной из важнейших составляющих этого процесса является осознание ребенком законов окружающе­го мира природы и способах ...

Структура разрабатываемого портфолио
Для начала перечислим принципы, которые лежат в основе предлагаемой нами концепции электронного портфолио: - электронное портфолио должно соотноситься с ФГОС, его некоторыми концепциями; - механизмы формирования электронного портфолио должны корреспондироваться с ожиданиями педагогической обществен ...

Формы организации обучения дошкольников родному языку в дошкольном учреждении
Обучение родному языку в дошкольных учреждениях осуществляется в двух формах: в повседневной жизни и на специально организованных занятиях. В повседневной жизни обеспечиваются условия для максимальной реализации потребности ребенка в речевом общении с взрослыми и сверстниками. Здесь можно отметить ...