Методические подходы к изучению действия умножения

На основе этого правила, используемого как прием счета, составляется таблица умножения на 2.

Например:

Используя таблицу умножения числа 2, вычисли и запомни таблицу умножения на 2:

2*3 =6 3*2 =…

2*4 =8 4*2 =…

2*5 =10 5*2 =…

2*6 =12 6*2 =…

2*7 =14 7*2 =…

2*8 =16 8*2 =…

2*9 =18 9*2 =…

На основе этого же приема составляется таблица умножения на 3:

3*4 =12 3*7 =21 4*3 =… 7*3 =…

3*5 =15 3*8 =24 5*3 =… 8*3 =…

3*6 =18 3*9 =27 6*3 =… 9*3 =…

Составление двух первых таблиц распределяется на два урока, что соответственно увеличивает время, отведенное на их заучивание. Каждая из двух последних таблиц составляется на одном уроке, поскольку предполагается, что дети, зная исходную таблицу, не должны отдельно заучивать результаты таблиц, полученных с помощью перестановки множителей.

На самом деле, многие дети учат каждую таблицу отдельно, поскольку недостаточный уровень развития гибкости мышления не позволяет им легко перестроить модель заученной схемы табличного случая в обратном порядке.

Для запоминания таблицы умножения существуют такие приемы как:

- прием счета двойками, тройками, пятерками;

- прием последовательного сложения – основной прием получения результатов табличного умножения. Данный прием связан со смыслом действия умножения как сложения одинаковых слагаемых;

- прием прибавления слагаемого к предыдущему результату (вычитания из предыдущего результата).

- прием взаимосвязанной пары: 2*6 6*2 (перестановка множителей);

- прием запоминания последовательности случаев с ориентиром на возрастание второго множителя;

- прием «порции»;

- прием запоминающегося случая в качестве опорного. Например, 5*6 =30, значит 5*7 =30+5 =35;

- прием внешней опоры; В качестве опоры используется рисунок или прямоугольная таблица чисел. Детям, которые обладают плохой механической памятью, можно па первых порах предложить использовать клетчатое поле тетради. Обводя на клетчатом поле прямоугольник с заданным количеством клеток в сторонах, ребенок использует эту модель для контроля полученного результата или просто подсчитывает клетки как умеет. Например:

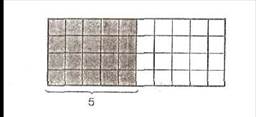
4 * 5 = 20

- прием запоминания таблицы «с конца»;

- пальцевый счет при запоминании таблицы умножения. Например, нужно умножить 6 на 7. Зажимаем пальцы на обеих руках в кулак, а затем на каждой руке отгибаем столько пальцев, на сколько каждый множитель больше, чем пять. На двух руках отогнуто три пальца - это число десятков в искомом числе. На одной руке остались прижатыми к ладони три пальца, на другой — четыре пальца. Эти числа перемножаем 3 * 4 = 12 и прибавляем к числу имеющихся десятков. 30 + 12 = 42. Ответ: 6 * 7 = 42.

Смысл действия деления

Действие деления рассматривается в начальной школе как действие, обратное умножению.

Деление – это обратное умножению математическое действие: нахождение одного из сомножителей по произведению и другому сомножителю. [Ожегов]

С теоретико-множественной точки зрения смыслу деления соответствует операция разбиения множества на равночисленные подмножества. Таким образом, процесс нахождения результатов действия деления связан с предметными действиями двух видов:

а) разбиение множества на равные части (например, 8 кружков разложили в 4 коробки поровну — раскладывают 8 кружков по одному в 4 коробки, а затем считают, сколько кружков получилось в каждой коробке);

б) разбиение множества на части по сколько-то в каждой части (например, 8 кружков разложили в коробки по 4 штуки — раскладывают 8 кружков по 4 штуки в коробки, а затем считают, сколько получилось коробок; деление по этому принципу в методике называют «деление по содержанию»).

Используя подобные предметные действия и рисунки, дети находят результаты деления.

Выражение вида 12 : 6 называют частным.

Число 12 в этой записи называют делимым, а число 6 – делителем.

Запись вида 12 : 6 = 2 называют равенством. Число 2 называют значением выражения. Поскольку число 2 в данном случае получено в результат деления, его также называют частным.

В начальной школе действие деления рассматривают как действие обратное умножению. В связи с этим сначала дети знакомятся со случаями деления без остатка в пределах 100 — так называемым табличным делением, С действием деления дети знакомятся после того, как уже выучили наизусть таблицы умножения чисел 2 и 3, На основе знания этих таблиц уже на четвертом уроке после знакомства с делением, составляется первая таблица деления на 2. Для получения ее значений используют предметный рисунок.

2:2 =… 8:2 =… 14:2 =…

4:2 =… 10:2 =… 16:2 =…

6:2 =… 12:2 =… 18:2 =…

Значения частных в этой таблице получают подсчетом элементов рисунка на картинке.

Следующая таблица деления — деление не 3 является последней таблицей, изучаемой во втором классе. Составляется эта таблица на основе взаимосвязи компонентов умножения с использованием правила нахождения неизвестного множителя. В связи с тем, что данное правило в явном виде предлагается детям в полной формулировке только в 3 классе, на этапе составления таблицы деления на 3 по-прежнему целесообразнее опираться на предметную модель действия (модель на фланелеграфе или рисунок).

Информация по педагогике:

Фольклорные занятия в воспитании
Педагогикой издавна осознавалась важность народного творчества для общего развития ребенка и необходимость применения его в воспитании. Но каждый исторический период выдвигает на первый план свои задачи. В наше время наиболее активной является проблема сохранения национальных традиций, установление ...

Теоретическая поддержка темы «Бериллий»
Соединения бериллия в виде драгоценных камней были известны еще в древности. С давних пор люди искали и разрабатывали месторождения аквамаринов, изумрудов и бериллов. Есть свидетельства о том, что еще во времена Египетских фараонов разрабатывались изумрудные прииски в Аравийской пустыни. Но только ...

Состояние экологического образования в общеобразовательных школах Республики Беларусь
В Беларуси с учётом мирового опыта была разработана и внедряется Концепция образования в области окружающей среды. Она опирается на ведущие международные и отечественные документы. Для обеспечения реализации на практике основных положений Концепции образования в области окружающей среды разработана ...