Анализ средств решения знаменитых задач древности

Задача о трисекции угла

Требуется произвольный угол разделить на три равные части.

Деление прямого угла

Пользуясь циркулем и линейкой, древние греки умели делить произвольный угол на две равные части. Со времен Пифагора они умели делить прямой угол на три равные части. Это они выполняли так. Поручень ограждение по материалам www.medimet16.ru.

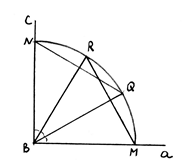
Пусть дан прямой угол АВС и требуется разделить его на три равные части, т.е. произвести трисекцию этого угла. Для этого из вершины данного угла В, как из центра, проводим окружность (для нужного построения достаточно провести четверть окружности). Точки пересечения окружности со сторонами АВ и ВС соответственно обозначим через М и N. Далее из точек М и N тем же радиусом делаем засечки R и Q. Теперь соединим хордами M и R, N и Q. Получаем два равносторонних треугольника ∆BRM и ∆BQN. Но в равностороннем треугольнике все три угла по 60о.

Следовательно, ∟MBR=∟QBN=60о. Тогда ∟MBQ=∟RBN=∟QBR=30о. Итак, данный прямой угол удалось разделить на 3 равные части.

Возможные построения

Чтобы иметь хотя бы некоторое представление о разрешимости и неразрешимости задач на построение, ограничимся следующим небольшим замечанием. Прежде всего, напомним, что при помощи циркуля и линейки можно сравнительно легко построить выражения:

где a, b, c суть данные или найденные отрезки.

Если решение задачи сводится к последовательному выполнению конечного числа этих операций, то задача оказывается разрешимой при помощи циркуля и линейки. Если же решение задачи не ограничивается последовательным выполнением указанных выше операций в конечном числе, то такую задачу при помощи циркуля и линейки решить невозможно. Задача о трисекции угла и является примером такой задачи, которую нельзя решить, прибегая только к циркулю и линейке, т. е. путем проведения окружностей и прямых линий.

Доказательство неразрешимости

Древнегреческие ученые без особого труда делили произвольный угол на три равные части с помощью разного рода механизмов. Но перед ними всегда стоял вопрос: почему трисекция угла, легко выполнимая при помощи специально изготовленных механизмов, не поддается разрешению при помощи циркуля и линейки. И вообще разрешима ли эта задача в общем виде при помощи таких классических чертежных инструментов?

Чтобы ответить на поставленный вопрос, приведем некоторые рассуждения. Обозначим данный угол, который требуется разделить на три равные части, через 3α. Рассмотрим cos3α. По известным формулам тригонометрии

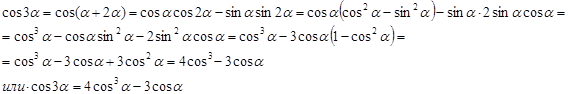
Умножая левую и правую части полученного равенства на 2, получаем

.

Пусть теперь 2 cos 3α = а и 2cos α = x, тогда

а = x3-3x или х3—Зx— а = 0. (1)

Чтобы доказать, что задача о трисекции угла неразрешима в общем виде при помощи циркуля и линейки, достаточно указать хотя бы один угол, который нельзя разделить при помощи циркуля и линейки. Путем несложных рассуждений покажем, что таким свойством обладает, например, угол в 60°. Действительно, полагая 3 а = 60°, получим cos 3 a = 1/2, и уравнение (1) примет вид

х3 — Зх — 1 =0. (2)

В алгебре доказывается, что рациональными корнями уравнения могли бы быть +1 и —1, но ни то, ни другое указанному уравнению не удовлетворяет. Выходит, что уравнение не имеет рациональных корней и, следовательно, по теореме неразрешимости (приложение 1) угол в 60° нельзя разделить на три равные части при помощи циркуля и линейки. Заметим, из того, что угол в 60° не может быть разделен на три равные части при помощи циркуля и линейки, вытекает, что угол в 20°, а следовательно, и угол в 40° не могут быть построены с помощью указанных инструментов. Отсюда вытекает важное следствие: правильный девятиугольник, восемнадцатиугольник и т. д. не могут быть построены циркулем и линейкой.

Далее, для а уравнения можно было бы указать еще бесчисленное множество значений, для которых уравнение неразрешимо в квадратных радикалах, и, следовательно, существует бесчисленное множество углов, трисекция которых не может быть выполнена при помощи циркуля и линейки.

Информация по педагогике:

Общие проблемы культуры речи
В последние годы вопросы речевой культуры горячо обсуждаются не только специалистами (лингвистами, методистами и преподавателями русского языка), но и широкой общественностью. Этой теме посвящаются радио- и телепередачи, статьи в газетах и журналах. Речь наших современников многими воспринимается и ...

Формы организации обучения дошкольников родному языку в дошкольном учреждении
Обучение родному языку в дошкольных учреждениях осуществляется в двух формах: в повседневной жизни и на специально организованных занятиях. В повседневной жизни обеспечиваются условия для максимальной реализации потребности ребенка в речевом общении с взрослыми и сверстниками. Здесь можно отметить ...

История интеграции
Интегрирование детей с особенностями развития в общество как социальное явление насчитывает несколько столетий. История специального образования показывает, что идея совместного обучения детей с проблемами в учебе и детей с нормой развития существует с 70-х годов, когда европейскому обществу удалос ...