Анализ средств решения знаменитых задач древности

Итак, если пользоваться только циркулем и линейкой, задача о трисекции угла в общем виде неразрешима.

Разрешимость для некоторых углов

Древним ученым, как указывалось выше, была известна трисекция прямого угла при помощи циркуля и линейки. Возможность этой трисекции можно подтвердить и теоретически. Действительно, положив 3 α =90°, получим, что а = 0, и уравнение примет вид

х3-3х=0. (3)

Уравнение (3) имеет корни О, . Таким образом, ненулевые корни выражены в квадратных радикалах. Следовательно, угол в 90° можно разделить циркулем и линейкой на три равные части.

Рассуждая аналогично, можно было бы показать, что теми же средствами и угол в 45° можно разделить на три равные части. Необходимо добавить, что трисекция при помощи циркуля и линейки возможна для Бесчисленного множества углов, например для углов вида , где п—целое положительное число.

Решение Архимеда

Оригинальное и вместе с тем чрезвычайно простое решение задачи о трисекции угла при помощи циркуля и подвижной линейки с двумя отметками дал Архимед. Как это делается, покажем на конкретном примере. Пусть требуется произвольно взятый острый угол AВС разделить на три равные части. Для этого из вершины данного угла В, как из центра, произвольным радиусом R опишем окружность (рис. 2).

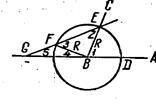
Точки пересечения сторон данного угла с окружностью обозначим через D и Е. Теперь берем подвижную линейку с двумя точечными отметками F и G, причем длина отрезка FG = R, и прикладываем ее к точке Е так, чтобы F и G оказались на одной прямой с точкой Е и чтобы F находилась на окружности, а G — на продолжении стороны ВА. Тогда угол: ЕGD и будет составлять одну треть заданного угла АВС. Докажем это.

Обозначим, для краткости углы на чертеже цифрами 1, 2, 3, 4, 5. Надо доказать, что угол 5 составляет третью часть угла 1, т. е. <5=1/3<1.

Действительно, <1 = <5 + <2 (свойство внешнего угла треугольника), но <3 = <5 + <4 (свойство внешнего угла треугольника). Далее, <5 = <4 (свойство равнобедренного треугольника). Тогда <3 =2<5 . Из равнобедренного треугольника ВЕF <3=<2. Учитывая предыдущее равенство, будем иметь

<1=<3+<5=2<5+<5=3<5.

Следовательно, <5=1/3<1, что и требовалось доказать.

Решение при помощи квадратрисы

В середине примерно пятого века до нашей эры Гиппий Элидский открыл новую кривую, которая была построена для деления данного угла на любое количество частей.

Пусть дан острый угол α и требуется разделить его на три равные части.

Сначала построим для некоторого квадрата АВСД квадратрису (рис. 3). Для этого дугу окружности ДВ и сторону АВ данного квадрата делим на 2n равных частей, где n – любое натуральное число. Заметим, что чем больше возьмем n, тем точнее будет построение квадратрисы. Для простоты положим n=4, тогда 2n=8. Делим дугу ДВ и радиус АВ на 8 равных частей. Концы полученных равных частей дуги ДВ обозначим цифрами 1, 2, 3, 4, 5, 6, 7.

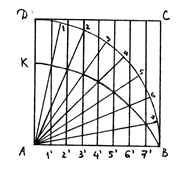
Точки деления неподвижного радиуса АВ обозначим через 1’, 2’, 3’, 4’, 5’, 6’, 7’. Теперь точки 1 – 7 соединим прямыми с точкой А, а через точки 1’ – 7’ проведем прямые, перпендикулярные АВ.

Точки пересечения полученных радиусов с соответствующими прямыми, перпендикулярными АВ, и будут точками квадратрисы. Соединяя эти точки плавной кривой, мы и получаем квадратрису КВ, как непрерывную линию.

Теперь при помощи квадратрисы разделим заданный острый угол α на три равные части. Для этой цели построим угол FAB, равный углу α (рис. 4).

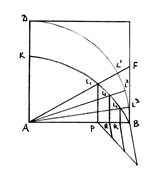
Обозначим точки пересечения прямой AF с квадратрисой KB и окружностью DB соответственно через L1 и L1. Далее из точки L1 на прямую AB опустим перпендикуляр L1P. Затем отрезок PB обычным приемом, показанным на чертеже, разделим на 3 равные части точками Q и R. В точках Q и R к прямой AB восстановим перпендикуляр до пересечения их с квадратрисой KB в точках L2 и L3. Соединяя точки L2 и L3 с точкой A и продолжая прямые AL2 и AL3 до пересечения с окружностью DB , получим точки L2 и L3.

Информация по педагогике:

Состояние экологического образования в общеобразовательных школах Республики Беларусь
В Беларуси с учётом мирового опыта была разработана и внедряется Концепция образования в области окружающей среды. Она опирается на ведущие международные и отечественные документы. Для обеспечения реализации на практике основных положений Концепции образования в области окружающей среды разработана ...

Характеристика уровня развития представлений о форме предметов у детей подготовительной к школе группы на констатирующем этапе эксперимента
Цель констатирующего эксперимента: выявление уровня развития представлений о форме предметов у детей контрольной и экспериментальной групп. В качестве основного метода исследования использовалась диагностика математического развития Т.С. Комаровой и О.А. Соломенниковой. Диагностика по методике сост ...

Межнациональное общение как педагогический феномен
Человек формируется как личность в определенной системе общественных отношений (в том числе и национальных), усваивая принятые в обществе нормы и правила, которые определяют в дельнейшем его линию поведения и поступки. Однако из этого не следует, что личность - пассивный продукт внешних воздействий ...