Анализ средств решения знаменитых задач древности

Поскольку а, х, у, 2а — геометрическая прогрессия, то

,

откуда х2 = ау и у2 = 2ах. Следовательно, х4 = a2y2 = 2a3x или х3 = 2а3. Выходит, что х и есть ребро искомого куба, превосходящего по объему данный куб с ребром а в два раза.

Ясно, что при помощи циркуля и линейки «вставки» х и у найти нельзя, так как обратное приводило бы к построению циркулем и линейкой х = , что, как указывалось выше, выполнить невозможно.

Решение Платона

Оказывается, «вставки» х и у можно найти, если воспользоваться дополнительными средствами в виде специально изготовленных приборов (механизмов). Оригинальные и весьма простые приборы для механического нахождения «вставок» х и у по двум заданным отрезкам а и 2а предложили Платон и Эратосфен. Прибор Платона состоит из двух обыкновенных прямоугольных плотничьих наугольников, а само построение основано на лемме:

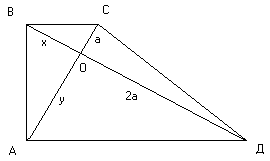
Лемма: Во всякой прямоугольной трапеции с перпендикулярными диагоналями, отрезки диагоналей образуют геометрическую прогрессию:

Доказательство: Пусть АВСД – прямоугольная трапеция, у которой ∟А=∟В=90о и АС перпендикулярно ВД. В этом случае докажем, что . Из того, что ∆АВС и ∆ВАД прямоугольные, а ОВ и ОА соответственно их высоты, вытекает:

(1)

(2).

Из (1) и (2), как следствие, получаем: . Что и требовалось доказать.

Построение «вставок» х и у, нужных для решения задачи об удвоении куба, проводится следующим образом. Берутся две взаимно перпендикулярные прямые т и п, пересекающиеся в точке О (рис. 7).

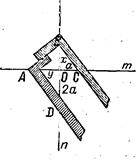
На прямой т вправо от точки О отложим отрезок ОС = а (а — сторона куба, подлежащего удвоению). На прямой п вниз от точки О отложим отрезок OD = 2а. Теперь возьмем два прямоугольных плотничьих наугольника (на чертеже заштрихованы) и расположим их так (см. рисунок), чтобы сторона первого наугольника проходила через точку С, которая считается данной, а вершина его находилась на прямой п; чтобы сторона второго наугольника проходила через точку D, которая также считается данной, а вершина находилась бы на прямой m; остальные две стороны наугольников должны соприкасаться.

При таком расположении двух наугольников по данным точкам С и D найдем на прямых т и п точки А и В. Тогда 0В = х, а О А = у. По лемме

, откуда .

Следовательно, х = 0В и есть построенное ребро удвоенного куба, что и нужно было сделать.

Решение Эратосфена

Прибор Эратосфена носит название «мезолябий», что в переводе означает «уловитель», т. е. уловитель двух средних величин («вставок»), из которых одна составляет искомую сторону удвоенного куба.

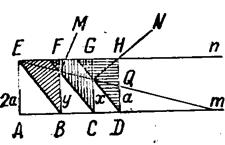
Мезолябий Эратосфена состоит из двух параллельно расположенных реек т и п, расстояние между которыми равняется удвоенной стороне куба, т. е. 2а. К этим рейкам прикреплены три равных прямоугольных треугольника, из которых один, самый левый, смонтирован неподвижно, а другие два могут перемещаться вдоль пазов, устроенных в рейках, причем на верхнюю рейку опираются равные катеты, а на нижнюю — их противоположные вершины (рис. 8).

На катете HD самого правого подвижного треугольника откладываем отрезок DQ = а. Теперь двигаем подвижные треугольники с таким расчетом, чтобы точки пересечения катета одного треугольника с гипотенузой следующего за ним (М и N) расположились бы на одной прямой с Е и Q. Тогда из соответствующих подобных треугольников получаем

Информация по педагогике:

Активизация учебного процесса
Учебный процесс в современной начальной школе, утверждал Дьюи, противоестествен природе ребенка, его стремлению делать и знать. Школа заставляет детей сидеть часами неподвижно и выслушивать, молчаливо впитывать сложные и непонятные факты. Следствием такого процесса обучения является нелюбовь детей ...

Семейные факторы, влияющие на развитие ребенка
Родительское воспитание при определенных условиях может быть неблагоприятным когда ребенок воспитывается одним родителем, приемными родителями, отчимом или мачехой, родственниками, чужими людьми, а также родителями при непостоянном с ними проживании. Воспитание в неполной семье, в частности, станов ...

Знакомство с понятием площади
Как уже упоминалось выше понятие площади (и ее измерения) базируется на ряде других понятий. Знакомство с площадью в пятом классе начинается с изучения площади прямоугольника. Учащимся предлагается конструктивное определение площади. Хотя определением его назвать можно с трудом, скорее это правило ...