Анализ средств решения знаменитых задач древности

.

Обозначая NC через х и MB через у, находим .

Следовательно, х = NC и будет найденной величиной искомого ребра удвоенного куба. Делосская задача решена.

Решение Менехма

1) Решение задачи об удвоении куба с ребром а сводится к рассмотрению двух парабол: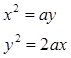

Решая эти уравнения, как систему относительно x, будем иметь

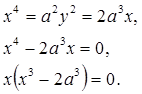
Получаем 2 вещественных корня 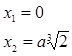. Первый корень не удовлетворяет условию задачи. Следовательно, искомым решением будет второй корень, т.е. ребро удвоенного куба равняется .

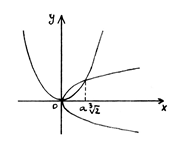
Путем построения графиков обеих парабол искомое ребро куба получается, как ненулевая абсцисса точки пересечения парабол:

2) Задача об удвоении куба сводится к решению двух уравнений, из которых одно – уравнение гиперболы, а другое – уравнение параболы

.

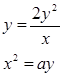Решая совместно относительно х, получим 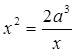, или . Следовательно, . Путем построения графиков искомое ребро удвоенного куба находится, как абсцисса пересечения гиперболы с параболой:

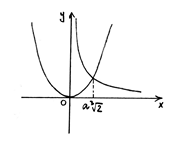
Задачу об удвоении куба можно предлагать не ранее чем в восьмом классе, т.к. основным в решении является понятие иррационального числа. Кроме того, решение задачи опирается на изучаемые в восьмом классе теорему Пифагора и решение рациональных и иррациональных уравнений. Этот материал занимает прочное место и большой объем в курсе математики в восьмом классе, и дать его детям раньше представляет определенную трудность.

Учащиеся должны знать, что такое иррациональное число, что оно не выражается конечной или бесконечной периодической дробью, уметь извлекать квадратный корень, иметь представления о решении рациональных уравнений, должны знать формулировку теоремы Пифагора, уметь использовать ее.

Из того, что для построения ребра удвоенного куба необходимо построить , следует, что дети должны уметь извлекать корни n-й степени, в частности, корень кубический. Этот материал изучается в девятом классе.

Прежде, чем давать в рассмотрение задачу об удвоении куба, необходимо убедиться, что детям известны возможные построения циркулем и линейкой. Если же этого нет, то нужно обязательно предоставить детям возможность изучить этот материал, самостоятельно или с помощью учителя. Без этого знания учащиеся не смогут понять, почему при помощи циркуля и линейки построить нельзя. А это необходимое условие для дальнейшего продвижения в решении задачи.

Теорема неразрешимости не изучается в курсе школьной математики, поэтому ее формулировку и пояснение ее смысла следует давать детям дополнительно. Это возможно не ранее, чем в девятом классе, так как в теореме идет речь о кубическом уравнении, не имеющем рациональных корней.

Для понимания рассуждений о построении «вставок» требуется знание геометрической прогрессии, пропорций и их свойств. Это также указывает на невозможность изучения задачи до девятого класса, потому что именно в девятом классе проходят геометрическую прогрессию.

О геометрической прогрессии нужно знать: ее определение и следующее свойство – отношение двух, следующих друг за другом, членов геометрической прогрессии постоянно. О пропорции также нужно знать определение и свойство – произведение крайних членов пропорции равно произведению ее средних членов.

Информация по педагогике:

Межнациональное общение как педагогический феномен
Человек формируется как личность в определенной системе общественных отношений (в том числе и национальных), усваивая принятые в обществе нормы и правила, которые определяют в дельнейшем его линию поведения и поступки. Однако из этого не следует, что личность - пассивный продукт внешних воздействий ...

Программа исследования по профилактике девиантного поведения подростков
Данное исследование проводилось в г. Костомукша на базе Центра социальной помощи семье и детям «Надежда» с 1 по 21 ноября 2010 года. Основная цель исследования: Рассмотреть социально-негативные проявления подростков и изучить процесс социально-профилактической работы по предупреждению девиантного п ...

Современные педагогические средства как основа развития учебной мотивации студентов
Логика нашего исследования предполагает рассмотрение вопроса "какие современные средства обучения рациональней всего использовать для развития учебной мотивации студентов УСПО?". В данном параграфе мы к ним и обратимся. Нельзя говорить о современных педагогических средств обучения, не зат ...