Анализ средств решения знаменитых задач древности

Не в состоянии решить эту задачу так, как требовал оракул, делосцы обратились за помощью к математику и философу Платону. Но он уклончиво ответил им: «Боги, вероятно, недовольны вами за то, что вы мало занимаетесь геометрией». Однако сам Платон не сумел решить указанной задачи циркулем и линейкой. С того времени эта задача и стала именоваться «делосской» (иногда ее неправильно называют «делийской»).

Удвоение квадрата

Древние греки сравнительно легко решили задачу об удвоении квадрата. Для этого надо было уметь строить при помощи циркуля и линейки корень квадратный из двух. Действительно, если сторона данного квадрата равняется а, а сторона искомого квадрата х, то, согласно условию задачи, будем иметь , откуда .

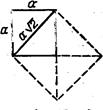
Следовательно, в качестве х надо взять диагональ данного квадрата, которая по теореме Пифагора как раз и будет равняться (рис. 5).

Сведение задачи к нахождению

Обобщая задачу об удвоении квадрата, древние греки перешли к рассмотрению задачи об удвоении куба и также стремились решить ее при помощи циркуля и линейки. Оказалось, что решение задачи об удвоении куба сводится к построению циркулем и линейкой корня кубического из двух. Действительно, если ребро данного куба положить равным а, а ребро искомого куба х, то, согласно условию задачи, будем иметь

х3 = 2а3, откуда .

Однако все старания построить циркулем и линейкой не увенчались успехом. И трудно сказать, как долго еще продолжались бы эти попытки, если бы, наконец, в первой половине XIX в. не было доказано, что при помощи только циркуля и линейки построить нельзя.

Доказательство неразрешимости

В современной математике доказано, что кубическое уравнение с рациональными коэффициентами, не имеющее рациональных корней, не может быть разрешимо в квадратных радикалах, т. е. ни один из корней этого уравнения не может быть построен при помощи циркуля и линейки.

Доказательство этой теоремы в приложении 1.

Выше было показано, что задача об удвоении куба сводится к решению кубического уравнения , где а — ребро данного куба, х — искомое ребро удвоенного куба.

Приняв для простоты длину ребра данного куба за 1, получим уравнение х3 — 2=0. Это уравнение с рациональными коэффициентами, как легко убедиться, не может иметь рациональных корней. Следовательно, по предыдущей теореме задача об удвоении куба не может быть решена при помощи циркуля и линейки.

Первым из ученых, открыто высказавшим мнение о невозможности построения посредством циркуля и линейки отрезка, равного , был французский ученый Р. Декарт. В 1637 г. он высказал предположение, что корень кубический из некубического рационального числа есть вообще иррациональность, не приводящаяся к конечному числу действий извлечения квадратного корня.

Строгое доказательство неразрешимости задачи об удвоении куба при помощи циркуля и линейки было дано французским математиком П. Венцелем в 1837 г.

Вклад в решение Гиппократа Хиосского

Одним из первых древнегреческих геометров, сделавших значительный шаг в решении задачи об удвоении куба путем привлечения к циркулю и линейке дополнительных средств, был Гиппократ Хиосский (V в. до н. э.).

Решение стереометрической задачи, какой является делосская задача об удвоении куба, Гиппократ Хиосский свел к рассмотрению планиметрической задачи, заключающейся в отыскании двух средних, пропорциональных между двумя данными отрезками, из которых второй в два раза больше первого. Т. е. к нахождению таких двух отрезков х и у, которые, будучи «вставлены» между двумя данными а и 2а, составили бы вместе с ними геометрическую прогрессию: а, х, у, 2а.

Информация по педагогике:

Социально-педагогические технологии профессиональной ориентации старшеклассников
Современная социально-экономическая ситуация в стране характеризуется разномасштабными преобразованиями во всех сферах жизни, что сопровождается активными процессами разрушения привычных взглядов, убеждений, установок, ценностных ориентации и замещения их новыми. В профессиональной сфере это проявл ...

Песня. Её роль в формировании иноязычных речевых навыков
Начнём с того, что комплексное развитие практических, образовательных, развивающих и воспитательных задач обучения возможно лишь при условии воздействия не только на сознание учащихся, но и на сферу их личных интересов, склонностей и мотивов. Музыка является одним из самых эффективных способов возд ...

Характеристика структуры и содержания экзаменационной работы по математике
Работа состоит из трех модулей: «Алгебра», «Геометрия», «Реальная математика». В модули «Алгебра» и «Геометрия» входит две части, соответствующие проверке на базовом и повышенном уровнях, в модуль «Реальная математика» - одна часть, соответствующая проверке на базовом уровне. При проверке базовой м ...