Методика введения средств решения знаменитых задач древности

Когда общий способ удается выделить, он озвучивается у доски и этот этап завершается.

Четвертый этап, решение задачи «Квадратура круга» при помощи квадратрисы.

Задача о квадратуре круга

Построить квадрат, площадь которого была бы равновелика площади данного круга.

Решение Динострата при помощи квадратрисы

Пусть ANB – четверть окружности, расположенной в квадранте АОВ, а АМС – квадратриса этого квадранта. Далее Динострат воспользовался соотношением, которое позднее было доказано Паппом Александрийским: АNВ : ОВ = ОВ : ОС, где С – конечная точка квадратрисы.

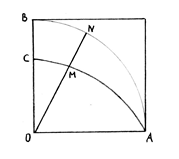
Поскольку ОА = ОВ = R, то ANB : R = R : OC, или

ANB = R2/OC. Откуда длина окружности радиуса R равняется 4R2/OC. Т.о. длина окружности определена. Чтобы построить квадрат равновеликий кругу, Динострат воспользовался теоремой: площадь круга равна площади треугольника, основание которого равно длине окружности, а высота – радиусу круга.

6. Подведение итогов.

В конце урока подвести итоги, обсуждая вопросы: что делали? Каких результатов добились?

Задача об удвоении куба

Вклад в решение Гиппократа Хиосского

Одним из первых древнегреческих геометров, сделавших значительный шаг в решении задачи об удвоении куба путем привлечения к циркулю и линейке дополнительных средств, был Гиппократ Хиосский (V в. до н. э.).

Решение стереометрической задачи, какой является делосская задача об удвоении куба, Гиппократ Хиосский свел к рассмотрению планиметрической задачи, заключающейся в отыскании двух средних, пропорциональных между двумя данными отрезками, из которых второй в два раза больше первого. Т. е. к нахождению таких двух отрезков х и у, которые, будучи «вставлены» между двумя данными а и 2а, составили бы вместе с ними геометрическую прогрессию: а, х, у, 2а.

Поскольку а, х, у, 2а — геометрическая прогрессия, то

,

откуда х2 = ау и у2 = 2ах. Следовательно, х4 = а 2y2 = 2 а 3x или х3 = 2 а 3.

Вопросы и задания.

Каким образом строятся «вставки»?

Чему равно ребро удвоенного куба, если ребро данного куба равно а?

Вычислить, чему равны «вставки» х и у при а:

А) 1, В) 4,

Б) 2, Г) 6.

Решение Платона

Прибор Платона состоит из двух обыкновенных прямоугольных плотничьих наугольников, а само построение основано на лемме:

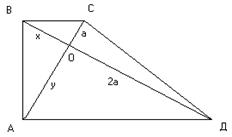
Лемма: Во всякой прямоугольной трапеции с перпендикулярными диагоналями, отрезки диагоналей образуют геометрическую прогрессию:

Построение «вставок» х и у, нужных для решения задачи об удвоении куба, проводится следующим образом. Берутся две взаимно перпендикулярные прямые m и n, пересекающиеся в точке О (см. рис.).

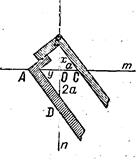
На прямой т вправо от точки О отложим отрезок ОС = а (а — сторона куба, подлежащего удвоению). На прямой n вниз от точки О отложим отрезок OD = 2а. Теперь возьмем два прямоугольных плотничьих наугольника (на чертеже заштрихованы) и расположим их так (см. рисунок), чтобы сторона первого наугольника проходила через точку С, которая считается данной, а вершина его находилась на прямой n; чтобы сторона второго наугольника проходила через точку D, которая также считается данной, а вершина находилась бы на прямой m; остальные две стороны наугольников должны соприкасаться.

Информация по педагогике:

Исследование межпредметных связей по дисциплине «История костюма и моды»
Одним из важнейших условий прочности и действенности формируемых у обучающихся знаний, умений и навыков является осуществление межпредметных связей в процессе преподавания дисциплины «История костюма и моды». Решение проблемы межпредметных связей играет важную роль при определении содержания, метод ...

Диагностика исходного уровня развития связной речи в ходе устного пересказа
Целью экспериментального исследования являлась разработка и апробация методики обучения пересказу как средства развития устной речи детей младшего школьного возраста. База исследования: прогимназия № 62 г. Новокузнецка, 2 "А" и "Б" классы. В каждом классе диагностировано по 12 д ...

Педагогические идеи
Дьюи неразрывно связаны с его философско-социальными взглядами. Преданный идеям демократии, болеющий на ее несовершенство, расслоение американского общества, тяготы миллионов простых людей, философ видел в образовании мощное средство развития подлинной демократии. «Единственным фундаментальным инст ...