Методика введения средств решения знаменитых задач древности

При таком расположении двух наугольников по данным точкам С и D найдем на прямых m и n точки А и В. х = ОВ и есть построенное ребро удвоенного куба.

Вопросы и задания.

Доказать лемму Платона.

Каким образом с помощью прибора Платона находятся «вставки»?

Доказать, что куб с ребром х в два раза больше по объему, чем куб с ребром а , т.е. х 3 = 2 а 3 (воспользоваться леммой).

Затем решается исходная задача, с помощью прибора Платона строится куб, в два раза больший по объему, чем куб с ребром:

А) 1, В) 4,

Б) 2, Г) 6.

Решение Эратосфена

Прибор Эратосфена носит название «мезолябий», что в переводе означает «уловитель», т. е. уловитель двух средних величин («вставок»), из которых одна составляет искомую сторону удвоенного куба.

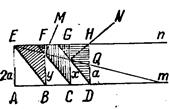
Мезолябий Эратосфена состоит из двух параллельно расположенных реек m и n, расстояние между которыми равняется удвоенной стороне куба, т. е. 2а.

К этим рейкам прикреплены три равных прямоугольных треугольника, из которых один, самый левый, смонтирован неподвижно, а другие два могут перемещаться вдоль пазов, устроенных в рейках, причем на верхнюю рейку опираются равные катеты, а на нижнюю — их противоположные вершины (см. рис.).

Решение

На катете HD самого правого подвижного треугольника откладываем отрезок DQ = а. Теперь двигаем подвижные треугольники с таким расчетом, чтобы точки пересечения катета одного треугольника с гипотенузой следующего за ним (М и N) расположились бы на одной прямой с Е и Q. х = NC и будет найденной величиной искомого ребра удвоенного куба.

Вопросы и задания.

Как устроен прибор Эратосфена?

Каким образом с помощью мезолябия находятся «вставки»?

Доказать, что куб с ребром х в два раза больше по объему, чем куб с ребром а , т.е. х 3 = 2 а 3.

С помощью прибора Эратосфена строится куб, в два раза больший по объему, чем куб с ребром:

А) 1, В) 3,

Б) 2, Г) 5.

Решение Менехма

1) Решение задачи об удвоении куба с ребром а сводится к рассмотрению двух парабол:

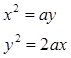
2) Задача об удвоении куба сводится к решению двух уравнений, из которых одно – уравнение гиперболы, а другое – уравнение параболы

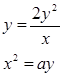
Вопросы и задания.

Каким образом задача сведена к рассмотрению функций?

Построить графики функций.

Найти с помощью графиков ребро удвоенного куба.

Задача о квадратуре круга

Решение Бинга

Приведем одно из решений задачи о квадратуре круга, основанное на использовании треугольника Бинга. Этот способ был предложен в 1836 г. русским инженером Бингом и очень удобен для практических целей.

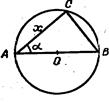
Рассмотрим треугольник АВС (см. рис.), вписанный в круг, квадратура которого находится с таким расчетом, чтобы наибольшая сторона треугольника была диаметром. Обозначим угол CAB через а, а хорду АС через х. Подберем угол а так, чтобы отрезок х был стороной квадрата, равновеликого данному кругу. Для этой цели воспользуемся соотношением

,

где R — радиус круга.

Так, как площадь квадрата со стороной х должна быть равновелика площади круга, то будем иметь или 4R2 cos2 a = πR2, откуда cos2 a =π/4, cos a =1/2 = 0, 886. По таблицам находим a=27°36'.

Информация по педагогике:

Объяснительно-иллюстративное обучение
Сообщающее или объяснительно-иллюстративное обучение характеризуется, прежде всего, тем, что учитель излагает знания в обработанном, «готовом» виде, ученики воспринимают и воспроизводят его. Это обучение как путь формирования знаний, несомненно, обладает достоинствами: подача и усвоение знаний осущ ...

Формы взаимодействия семьи по обучению детей старшего дошкольного возраста подвижным играм
Ни одна, даже самая лучшая физкультурно-оздоровительная программа не сможет дать полноценных результатов, если она не реализуется совместно с семьей, если в дошкольном учреждении не создано детско-взрослое общество (детей-родителей-педагогов), для которого характерно содействие друг другу, учет воз ...

Принципы русской орфографии
Природу русской орфографии обычно определяют с лингвистических позиций. Теоретические обобщения в области фонетики, графики, орфографии лежат в основе методики обучения грамоте и правописанию; грамматические теории (о частях речи, словосочетании, предложении) является базой для методики обучения гр ...