Методика введения средств решения знаменитых задач древности

Точки деления неподвижного радиуса АВ обозначим через 1’, 2’, 3’, 4’, 5’, 6’, 7’. Теперь точки 1 – 7 соединим прямыми с точкой А, а через точки 1’ – 7’ проведем прямые, перпендикулярные АВ.

Точки пересечения полученных радиусов с соответствующими прямыми, перпендикулярными АВ, и будут точками квадратрисы. Соединяя эти точки плавной кривой, мы и получаем квадратрису КВ, как непрерывную линию.

Ведущий строит квадратрису на доске, озвучивая каждое построение. Дети строят у себя в тетрадях, учитель проверяет, ходя между рядами.

После того, как дети выполняют построение, обсуждаются следующие вопросы:

У каждого ли квадрата есть квадратриса? Как она будет выглядеть примерно?

Зависит ли точность приближения от n меньше?

Возникающие вопросы и затруднения фиксируются, как возможные темы творческих работ.

Третий этап, решение задачи «Трисекция угла» при помощи квадратрисы.

В.: Квадратриса имеет очень интересные свойства. Давайте посмотрим, как с ее помощью можно разделить угол на три части. Мы видели, что эту задачу без квадратрисы нам решить не удалось. Но сначала мы рассмотрим деление заданного угла на две равные части.

Формулировка задачи записывается на доску. Ученикам раздаются шаблоны квадратрисы для облегчения построений. Ведущий подробно описывает каждый шаг, следит за тем, что ученики выполняют у себя в тетрадях.

Деление угла на две части при помощи квадратрисы.

Теперь при помощи квадратрисы разделим заданный острый угол α на две равные части. Для этой цели построим угол FAB, равный углу α.

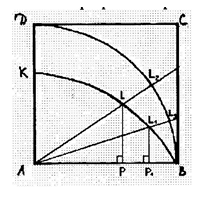
Обозначим точки пересечения прямой AF с квадратрисой KB и окружностью DB соответственно через L1 и L1. Далее из точки L1 на прямую AB опустим перпендикуляр L1P. Затем отрезок PB обычным приемом разделим на 2 равные части точкой Q. В точке Q к прямой AB восстановим перпендикуляр до пересечения его с квадратрисой KB в точке L2. Соединяя точку L2 с точкой A и продолжая прямую AL2 до пересечения с окружностью DB , получим точку L2.

Поскольку дуги L1L2 и L2В равны между собой, то соответственные им центральные углы L1AL2, L2AB также равны между собой и каждый из них равен α/2. (равным отрезкам неподвижного радиуса АВ при помощи квадратрисы соответствуют и равные дуги окружности ДВ).

Ведущий производит построение на доске, дети у себя в тетрадях. Затем детям раздаются описания построения на листочках, для облегчения следующего построения.

В.: Теперь давайте попробуем, опираясь на это построение, разделить тот же самый угол на три равные части. Подумайте, как это можно сделать.

Новая задача записывается на доску. Школьники работают самостоятельно.

Через некоторое время один из учеников показывает построение на доске. Если никто не смог разделить, то дается подсказка.

В.: Давайте обратим внимание на то, за счет чего удалось разделить угол на две равные части. Выделим необходимое для этого построение (деление отрезка на две равные части).

После того, как деление угла на три равные части произведено, дается и выносится на доску следующее задание:

Выделить общий способ деления произвольного угла на заданное количество частей при помощи квадратрисы.

Далее обсуждается вопрос, какие углы можно делить при помощи квадратрисы. Как разделить угол больше угла 45˚, но меньше острого угла, как разделить тупой угол.

Информация по педагогике:

Оценка уровня сформированности самостоятельности и трудолюбия у младших школьников
Чтобы оценить уровень самостоятельности и трудолюбия у младших школьников, мы провели анкетирование на базе МБОУДОД «Центр детского и юношеского туризма и экскурсий (юных туристов) им. Двужильного» г. Кемерово. В исследовании принимали участие ученики начальных классов. В анкетировании участвовало ...

Порядок проведения ЕНТ
ЕНТ проводится по четырем предметам: трем обязательным - казахс­кий или русский язык (язык обучения), математика, исто­рия Казахстана и одному из предметов по выбору, который является профильным для подступления в вузы в Сузы на ту или иную специальность. Единое национальное тестирование проводится ...

Методы и методики изучения особенностей памяти у детей дошкольного возраста с нарушениями слуха
Цель констатирующего эксперимента: изучение особенностей памяти детей дошкольного возраста с нарушением слуха с их нормально развивающими сверстниками. Для достижения поставленной цели предстояло решить следующие задачи: Апробировать комплекс психодиагностических методик для выявления особенностей ...