Анализ средств решения знаменитых задач древности

Таким образом, чтобы доказать неразрешимость задачи о квадратуре круга при помощи циркуля и линейки, необходимо установить невозможность указанными средствами построить произведение данного отрезка R на число , а для этого достаточно показать, - что или число π есть число трансцендентное. Заслуга Ф. Линдемана как раз и заключается в том, что он впервые в мировой науке вполне строго доказал, что π есть число трансцендентное, и тем самым окончательно установил невозможность решения задачи о квадратуре круга с помощью циркуля и линейки. Вот почему Ф. Линдемана называют «победителем числа π».

Решение Бинга

Выше было показано, что задача о квадратуре круга неразрешима при помощи циркуля и линейки, однако она становится, вполне разрешимой, если специально для нее расширить средства построения, если воспользоваться некоторыми специальными кривыми (например, квадратрисой). Средствами циркуля и линейки можно решить задачу о квадратуре круга только приближенно.

Ниже приведем одно из приближенных решений задачи о квадратуре круга, основанное на использовании треугольника Бинга. Этот способ был предложен в 1836 г. русским инженером Бингом и очень удобен для практических целей.

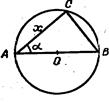
Рассмотрим треугольник АВС (рис. 11), вписанный в круг, квадратура которого находится с таким расчетом, чтобы наибольшая сторона треугольника была диаметром. Обозначим угол CAB через а, а хорду АС через х. Подберем угол а так, чтобы отрезок х был стороной квадрата, равновеликого данному кругу. Для этой цели воспользуемся соотношением

,

где R — радиус круга.

Так, как площадь квадрата со стороной х должна быть равновелика площади круга, то будем иметь или 4R2 cos2 a = πR2, откуда cos2 a =π/4, cos a =1/2 = 0, 886. По таблицам находим a=27°36'.

Итак, проводя в данном круге хорду под углом 27°36' к диаметру, мы сразу получим искомую сторону квадрата, равновеликого данному кругу. Легко догадаться, что рассмотренный треугольник АВС и есть треугольник Бинга.

Решение Динострата при помощи квадратрисы

Пусть ANB – четверть окружности, расположенной в квадранте АОВ, а АМС – квадратриса этого квадранта. Далее Динострат воспользовался соотношением, которое позднее было доказано Паппом Александрийским: АNВ : ОВ = ОВ : ОС, где С – конечная точка квадратрисы.

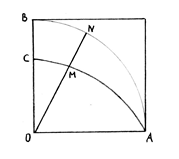
Поскольку ОА = ОВ = R, то ANB : R = R : OC, или

ANB = R2/OC. Откуда длина окружности радиуса R равняется 4R2/OC. Т.о. длина окружности определена. Чтобы построить квадрат равновеликий кругу, Динострат воспользовался теоремой: площадь круга равна площади треугольника, основание которого равно окружности, а высота – радиусу круга. Уравнение квадратрисы:

.

Для понимания рассуждений о неразрешимости задачи о квадратуре круга школьники должны знать формулу площади круга, изучаемую в девятом классе. Эту формулу вполне возможно объяснить детям на дополнительном занятии раньше. Следующее необходимое знание – это знание об иррациональных числах, изучаемое в восьмом классе. Также нужны дополнительные знания из теории геометрических построений о том, на какое число и при каких условиях можно умножить данный отрезок.

Для возможности построения квадратуры круга при помощи треугольника Бинга обязательно нужно изучение описанной окружности, необходимо знать ее определение и теорему, что около любого треугольника можно описать окружность. Этот материал находится в курсе геометрии восьмого класса. В девятом классе изучается косинус острого угла прямоугольного треугольника, а это также необходимо для решения задачи. Также детям должно быть известно иррациональное число , они должны уметь приближенно вычислять , и пользоваться тригонометрическими таблицами Брадиса. Все это изучается в восьмом классе. Для переноса этой задачи в седьмой класс, необходимо дать детям все эти сведения на дополнительных занятиях.

Информация по педагогике:

Организация исследования метода тестирования как средства педагогического контроля обученности старшеклассников
Для определения эффективности метода тестирования как средство педагогического контроля обученности старшеклассников в МОУ СОШ №4 поселка Пойковский Нефтеюганского района было проведено экспериментальное исследования. В эксперименте участвовали учащиеся 9-11 классов. Исследование проходило в три эт ...

Формы дистанционного образования
Методы и средства обучения относятся к сущностным характеристикам дидактического процесса. Они могут обеспечить достижение требуемых целей обучения, если будет в наличии необходимая для этого материально-техническая база, а преподавателю предоставят право выбора организационной стороны обучения, т. ...

Современное состояние проблемы изучения элементов теории множеств в начальном курсе математики
Работа с учебником «Математика-3», производится по программе «Школа 2000…». На ранних стадиях обучения, опираясь на житейский опыт учащихся и конкретные примеры, вводятся понятия множества и величины (при этом множества рассматриваются лишь непересекающиеся, а сам термин «множество» на первых порах ...