Показатели и критерии уровня овладения детьми исследовательской деятельностью

a) Назовите как можно больше предметов, которые одновременно являются и твердыми и прозрачными (возможные ответы: стекло, лед, кристалл, пластик)

b) Назовите как можно больше предметов, являющихся: блестящими, синими, твердыми.

Данное умение параллельно развивали и на математическом материале, используя задания на независимость количества вещества от формы сосуда, на сохранение количества вещества; на измерение протяженных материалов условной меркой, разными условными мерками; измерения одного и того же объекта или разных по величине разными мерками. Использование не только «линейных» измерений, но и жидких, и сыпучих веществ помогало формированию обобщенных представлений.

Например:

· Игровое упражнение «Измерь ленту»: детям предлагали измерить ленту разными по длине мерками – в начале короткой, а затем длинной или составленной из двух коротких.

Вопросы детям:

- Что изменилось, когда измерили во второй раз по сравнению с первым?

- Что осталось без изменения?

На этой основе дети формулировали выводы:

- когда мерка длиннее – число мерок меньше;

- когда мерка короче – число мерок больше;

- мерок уложилось больше – лента длиннее;

- мерок уложилось меньше – лента короче.

Для активации познавательной деятельности детей использовали вопросы: Почему?; Почему так получилось?; Объясни, как это получается.

Эти вопросы требовали самостоятельного обоснования характера зависимости между величинами.

С этой же целью детям предлагается ситуация «Как помочь повару?»

Сюжет: повар детского сада обращается к детям с просьбой – предложением: «Я знаю, что вы любите гречневую кашу. К сожалению, на кухне сломались весы. И я не могу узнать, сколько взять крупы для каши. Помогите мне. В каждую баночку (банки разного размера) нужно насыпать по одному бокалу крупы». Дети выполняют задание.

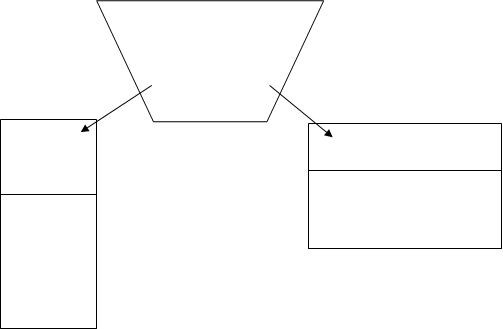Вопросы:

- В какой банке крупы больше? Почему?

Варианты ответов:

- крупы больше в высокой банке.

- крупы меньше в широкой банке.

- крупы в обеих банках поровну.

Решение проблемы: большинству детей кажется, что крупы больше в высокой банке. Часть детей утверждает, что крупы в обеих банках поровну. Появляются различные способы доказательства своего решения. Они начинают пересыпать крупу обратно в бокал (мерку), убеждаясь в равенстве количества крупы в разных банках. «Крупы в высокой и низкой банках одинаково, потому что в них насыпали по одному бокалу крупы». Другие, опираясь на собственные действия измерения, утверждают, что крупу «не добавляли» и «не убавляли». В банках по одному бокалу крупы.

Вывод: количество веществ (объем) сохраняется независимо от формы сосуда.

· В процессе работы мы использовали и такой метод, как загадки.

Например: «чем больше ты из нее берешь, тем больше она становится». (Яма).

- Что это?

- Так может быть? Когда?

Эта загадка вызывала затруднения. У детей в обычной жизни работает стереотип: чем больше берешь (конфет, игрушек), тем меньше остается. Загадка необычна тем, что противоречит стереотипу. Отгадать ее помогает практический эксперимент. Например, можно выкопать яму для растения. Решение приходит немедленно: «так, может быть, речь идет о яме».

Наблюдательность и внимание – важные составляющие исследовательской деятельности.

С этой целью использовались следующие задания:

a) Детям предлагалась карточки с фигурами для рисования.

Информация по педагогике:

Формы организации обучения дошкольников родному языку в дошкольном учреждении
Обучение родному языку в дошкольных учреждениях осуществляется в двух формах: в повседневной жизни и на специально организованных занятиях. В повседневной жизни обеспечиваются условия для максимальной реализации потребности ребенка в речевом общении с взрослыми и сверстниками. Здесь можно отметить ...

Закономерности обучения
Закономерности обучения – это существенные, устойчивые, повторяющиеся связи между составными частями, компонентами процесса обучения. Часть из них действует всегда, независимо от действий участников и условий процесса, например: цели и содержание обучения зависят от требований общества к уровню обр ...

Дидактико-методические основы обучения чтению иноязычных текстов
Знакомством культурой страны изучаемого языка было одной из главных задач еще со времен античности. Преподавание классических языков, как и трактовка религиозных текстов, не мыслится без культуроведческого комментирования. Временный государственный образовательный стандарт в число целей обучения ин ...